Introduction

This online software allows you to fit a value function, defined by a set of points, to a function that respects the constant trade-off attitude property

A value function is a function that assigns a value to a given performance. When using the MACBETH method, we can say that the obtained value functions are defined by a set of points in the form (performance, value). These value functions are thus defined in a piecewise linear way.

Regarding the shape of the value function, it can be classified as concave, convex or linear.

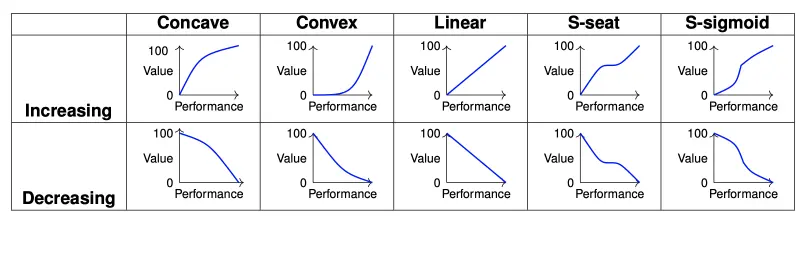
Methodology

The functions are defined as follows, with c being the trade-off attitude constant. On the left you can see the expressions and on the right the graphical representation of the functions. The function is fitted using the least squared differences method.

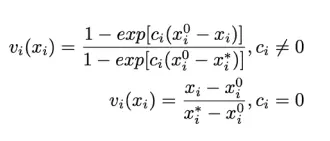Increasing Function:Decreasing Function: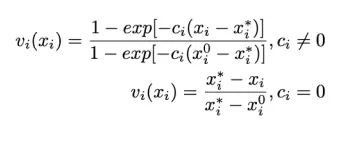

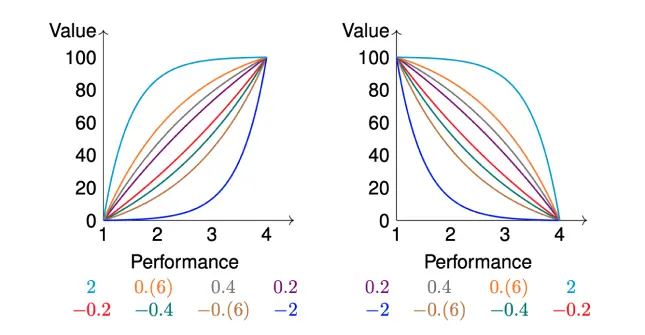
Graph of the delta function for different values of c (differently colored values of c correspond to differently colored lines in the graph). Increasing function on the left, decreasing function on the right.

Usage

To use the application, follow these steps:

1. Input the points as a list of pairs of (performance, value) in the box below.

   Example 1: (0, 100), (1, 37.5), (2, 12.5), (3, 0)

   Example 2: (0, 0), (1, 12.5), (2, 37.5), (3, 100)

2. Click the Fit Delta Function button and see the result in the graph.

Input

Result